Encrypting everything
From Gender and Tech Resources
Until it is destroyed [1], or we run out of resources to maintain its cables, bridges, root servers and data centers, or some idiot(s) replace(s) the current internet with a panopticon-like or a military-and-corporate-only global network, the web seems to be here to stay ... but it has an ad-hoc security model added post-hoc and it is up to us to make it better!?! WTF?
Before the digital age, the biggest users of cryptography were governments, particularly for military purposes.
With the advent of the net we can all use it for:
- Enabling authorised transactions.
- Defending free expression.
- Protecting our space, our objects and channels, from unauthorised access.
- Collectively failing at putting crypto into our own hands.


Contents
Crypto concepts

- The science of sending concealed messages is known as steganography (concealed writing). It is not very secure by itself. If someone finds the hidden message, all its secrets are revealed.
- Manipulating a message so that it can not be read even if it were intercepted is known as cryptography(hidden writing).
- Cryptography takes two forms: codes and ciphers.
- A code is essentially a secret language invented to conceal the meaning of a message, a system for hiding the meaning of a message by replacing each word or phrase in the original message with another character or set of characters (codegroups). The list of replacements is contained within a codebook. To protect a message in this way is called encoding. Encoding has no built-in flexibility.
- A cipherconceals a plaintext message by replacing or scrambling its letters. This process is known as enciphering and results in a ciphertext message. Converting a ciphertext message back to a plaintext message is known as deciphering. Each cipher can be split into two halves: the algorithm and the key. The key gives a cipher some built in flexibility.
- There are two classes of ciphers. A substitution cipher changes the letters in a message to another set of letters, or cipher alphabet, while a transposition cipher shuffles the letters around.
- Coded messages are often enciphered to improve their security, a process known as superencipherment.
- Encryption covers both the act of encoding and enciphering.
- Decryption covers both decoding and deciphering.
- Cryptotext covers both codetext and ciphertext but encicode is sometimes used instead.
- The science of breaking cryptotext or encicode is known as cryptanalysis.
- The two fields cryptography and cryptanalysis together make up the science of cryptology.
Most forms of cryptography used today rely on computers. Ciphers are better known today as algorithms, the guides for encryption -- they provide a way in which to craft a message and give a certain range of possible combinations. A key, on the other hand, helps a person or computer figure out the one possibility on a given occasion.
Checksums
Checksum
Probably one of the oldest methods of ensuring that data is correct, checksums also provide a form of authentication because an invalid checksum suggests that the data has been compromised in some fashion. A checksum is determined in one of two ways. Let's say the checksum of a packet is 1 byte long. A byte is made up of 8 bits, and each bit can be in one of two states, leading to a total of 256 (28) possible combinations. Since the first combination equals zero, a byte can have a maximum value of 255.
- If the sum of the other bytes in the packet is 255 or less, then the checksum contains that exact value.
- If the sum of the other bytes is more than 255, then the checksum is the remainder of the total value after it has been divided by 256.
Cyclic Redundancy Check (CRC)
CRCs are similar in concept to checksums, but they use polynomial division to determine the value of the CRC, which is usually 16 or 32 bits in length. The good thing about CRC is that it is very accurate. If a single bit is incorrect, the CRC value will not match up. Both checksum and CRC are good for preventing random errors in transmission but provide little protection from an intentional attack on your data. Symmetric- and public-key encryption techniques are much more secure.
Symmetric key encryption
In symmetric key cryptography (alias secret key cryptography) the same key is used to encrypt and decrypt the data.
There are many different algorithms using symmetric key cryptography, offering anything from minimal to nearly unbreakable security. Some of these algorithms offer strong security, easy implementation in code, and rapid encryption and decryption. Such algorithms are very useful for encrypting files stored on a computer to protect them in case an unauthorised individual gains access to the machine. They are somewhat less useful for sending messages from one computer to another, because both ends of the communication channel must possess the key and must keep it secure. Distribution and secure storage of such keys can be difficult and can open security vulnerabilities.
Symmetric ciphers have historically been susceptible to known-plaintext attacks, chosen plaintext attacks, differential cryptanalysis and linear cryptanalysis. Careful construction of the functions for each round can greatly reduce the chances of a successful attack.
Data Encryption Standard (DES)
The Data Encryption Standard is a popular symmetric-key encryption method developed in 1975 and standardised by ANSI in 1981 as ANSI X.3.92. DES uses a 56-bit key and uses the block cipher method, which breaks text into 64-bit blocks and then encrypts them.
DES is now considered to be insecure for many applications. This is mainly due to the 56-bit key size being too small; in January, 1999, Cryptography Research, Inc., Advanced Wireless Technologies, and the EFF collaborated to publicly break a DES key in 22 hours and 15 minutes [2].
Triple DES, also referred to as 3DES, is a mode of the DES encryption algorithm that encrypts data three times. Three 64-bit keys are used, instead of one, for an overall key length of 192 bits (the first encryption is encrypted with second key, and the resulting cipher text is again encrypted with a third key).
Advanced Encryption Standard (AES)
The Advanced Encryption Standard (alias Rijndael, its original name), is a specification for the encryption of electronic data established by the US National Institute of Standards and Technology (NIST) in 2001, replacing DES http://voip.kryptotel.net/aes-advanced-encryption-standard/. And was reported cracked in 2011 http://www.theinquirer.net/inquirer/news/2102435/aes-encryption-cracked. It involved a lot of cryptanalysis. Not likely happening on a daily basis, but possible.
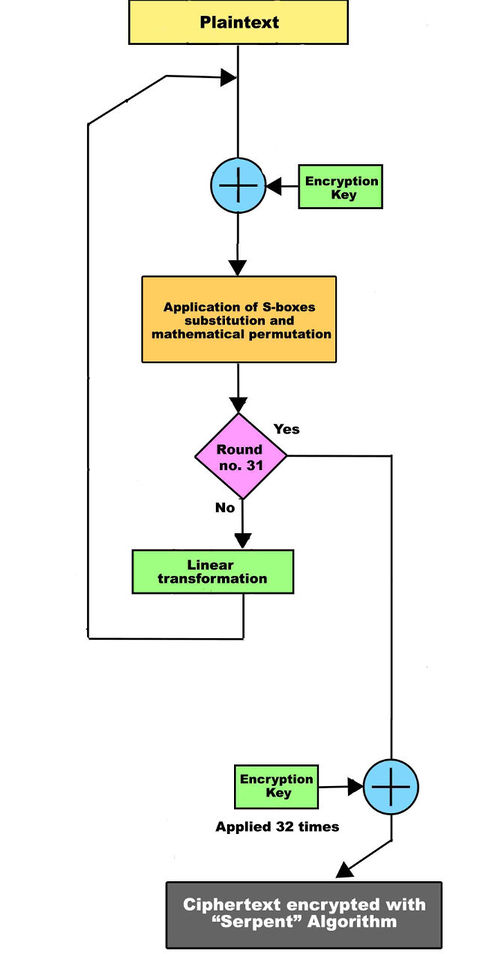
Serpent
Serpent also has a block size of 128 bits and supports a key size of 128, 192 or 256 bits.
The Serpent is a 128 bit block encryption that uses 32 rounds or 32 reiterations of the same algorithm using mathematical permutations and substitutions. The encrypting and decrypting phase have the same level of complexity. The decryption operations are exactly the inverted transformations used to encrypt the message but in opposite order. Serpent uses different mathematical substitutions "S-boxes" with a 4 bit entrance and a 4 bit exit. Every encryption phase uses an S-box that work collaterally for the 32 times.
The cipher is a 32-round substitution-permutation network operating on a block of four 32-bit words. Each round applies one of eight 4-bit to 4-bit S-boxes 32 times in parallel http://en.kryptotel.net/serpent.html. This maximizes parallelism, but also allows use of the extensive cryptanalysis work already done on DES.
The Serpent cipher is in the public domain and has not been patented. There are no restrictions or encumbrances whatsoever regarding its use. As a result, anyone is free to incorporate Serpent in their software (or hardware implementations) without paying license fees https://www.cl.cam.ac.uk/~fms27/serpent/.
Salsa20
The core of Salsa20 is a hash function with 64-byte input and 64-byte output. The hash function is used in counter mode as a stream cipher: Salsa20 encrypts a 64-byte block of plaintext by hashing the key, nonce, and block number and xor'ing the result with the plain text http://cr.yp.to/snuffle.html.
BLAKE2
The cryptographic hash function BLAKE2 https://blake2.net/ is an improved version of the SHA-3 finalist BLAKE. The core algorithm of BLAKE2 is derived from ChaCha, a stream cipher http://cr.yp.to/chacha.html
Twofish
Twofish has a 128-bit block size, a key size ranging from 128 to 256 bits, and is optimized for 32-bit CPUs. Currently there is no successful cryptanalysis of Twofish. Twofish is unpatented, and the source code is uncopyrighted and license-free; it is free for all uses. Full specifications, free source code, and other Twofish resources: https://www.schneier.com/twofish.html
Threefish
Threefish is a symmetric-key tweakable block cipher designed as part of the Skein hash function http://www.skein-hash.info/. Threefish uses no S-boxes or other table lookups in order to avoid cache timing attacks. Its nonlinearity comes from alternating additions with exclusive ORs.
Asymmetric key encryption
In asymmetric key cryptography (alias public-key encryption) different keys are used for encrypting and decrypting a message. The asymmetric key algorithms that are most useful are those in which neither key can be deduced from the other. In that case, one key can be made public while the other is kept secure. This provides some distinct advantages over symmetric encryption: the necessity of distributing secret keys to large numbers of users is eliminated, and the algorithm can be used for authentication as well as for cryptography.
Diffie-Hellman key agreement
The Diffie-Hellman key agreement algorithm was developed by Dr. Whitfield Diffie and Dr. Martin Hellman in 1976 to enable two parties who are involved in communication to generate a shared secret key for exchanging information confidentially. It uses modular arithmetic https://en.wikipedia.org/wiki/Modular_arithmetic.
Modulus or modulo (abbreviated as "mod") is the Latin word for "remainder, residue" or more in "what is left after parts of the whole are taken". Thus, "modular" or "mod arithmetic" is really "remainder arithmetic". For example:
- When 7 is divided by 3 it leaves a remainder of 1, thus: 7 mod 3 = 1
- When 8 is divided by 3 it leaves a remainder of 2: 8 mod 3 = 2
- When 9 is divided by 3 it leaves no remainder: 9 mod 3 = 0.
Now imagine the following scene from Wuthering Heights:
- Cathy and Heathcliff exchange public keys. These keys must have the same modulo portion, a prime
p. (see RFC 5114) - Cathy and Heathcliff each encrypt a shared, non-secret value,
g(also usually taken from RFC 5114), using their private keys, and they exchange these encrypted values. - Cathy encrypts the encrypted value received from Heathcliff with her private key, and vice versa. These values are used as a shared session key.
For example, Cathy says: 5,23 (base g = 5 and prime number p = 23, randomly chosen by Cathy)
O_/ 7_O_/
_/| ---------------5,23--------------> (/
__)\ /\/'
` \ 7
Cathy Heathcliff
Heathcliff chooses a private number = 6 and says (gmy private number mod p = 56 mod 23 =) 8
O_/ 7_O_/
_/| <----------------8---------------- (/
__)\ /\/'
` \ 7
Cathy Heathcliff
Cathy chooses private number = 15 and says (gmy private number mod p = 515 mod 23 =) 19
O_/ 7_O_/
_/| -----------------19--------------> (/
__)\ /\/'
` \ 7
Cathy Heathcliff
- Cathy received the 8 from Heathcliff, and thinks, (heathcliffs public number)my private number mod 23 = 815 mod 23 = 2. Aha! Now I know the key is 2.
- Heathcliff comes to a similar conclusion using what Cathy shouted from afar (19) for the world to hear: 196 mod 23 = 2.
- And both encrypt their communication with 2.
This solves the problem of how to pass a secret key between two parties without having any eavesdropper knowing the key. This does not solve the man in the middle attack (authentication): Someone can pretend to be Heathcliff and share a key with Cathy and Cathy will send encrypted information to "Heathcliff".
Rivest Shamir Adleman (RSA)
Ron Rivest, Adi Shamir, and Len Adleman released the Rivest-Shamir-Adleman (RSA) public key algorithm in 1978. This algorithm can be used for encrypting and signing data. The encryption and signing processes are performed through a series of modular multiplications http://mersennewiki.org/index.php/Modular_arithmetic.
It’s easy for a computer to multiply two large prime numbers together but if you gave this new number to a computer and asked it to tell you what prime numbers you multiplied to construct it, the computer would struggle. And the bigger the prime numbers get, the more the computer struggles, exponentially so. This is called a trapdoor, meaning it’s easy to go one way, but very hard to go the other. This mathematical difficulty is what ensures the strength of our encryption.
The RSA algorithm works as follows:
- Find two huge (at least 100 digits each!) prime numbers
pandq, and multiply them together to get the even bigger numbern. - Also combine p and q in a different way to generate another number e (details of this below).
- Publish these two numbers {n,e} as "public key", with the knowledge that there is enormous difficulty with even the world’s fastest computers breaking
ninto its constituent prime atomspandq. - The numbers {n,e} can be used by people to encrypt a message to send to me, and I can use my secret primes p and q to decrypt it.
In the unfolding love story, Heathcliff wants to encrypt and send Cathy his age (42 or forty-two). The RSA algorithm deals with sending numbers, but any text can be converted to digits in a variety of ways, so we can securely transmit information of any type.
- Cathy knows that Heathcliff wants to send her a message, so she selects two prime numbers, say p = 17 and q = 29 (n = p x q = 17 x 29 = 493).
- Cathy also needs to generate another number, e. She creates this number first by subtracting 1 off of each of her prime numbers p and q and then multiplies these two together ((p-1) x (q-1) = 448). This number is not e. The number e is allowed to be any number, which has no factors in common with this new number 448 (= 2 x 2 x 2 x 2 x 2 x 2 x 7). Now e is just any number which, when broken down into primes, does not possess a 2 or a 7 as a factor. There are lots of possibilities to choose from. Suppose Cathy picks e = 5.
- Cathy then gives the numbers n = 493 and e = 5 to Heathcliff.
- With these two numbers n and e, Heathcliff now encrypts his secret message: 42e mod n = 425 mod 493 = 42 x 42 x 42 x 42 x 42 mod 493 = 130,691,232 mod 493 = 383
- Cathy has received the number 383 from Heathcliff and needs to decrypt it to read it. Her first step, is to use her secret prime numbers p and q and the public number e to form another number d, which she can use to decrypt Heathcliff’s message. Cathy lists the multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40 ... and the multiples of 448: 448, 896, 1344, 1792, 2240, 2688 ... to find a number in the first sequence which is exactly one more than a number in the second sequence. That is the 269th term which is 1345, one more than the 3rd term 1344 in the 448 sequence. d = 269.
- Now Cathy can decode the message by doing one big calculation. She has Heathcliff's encrypted number, 383, and her new number, d = 269. The plaintext message = (ciphertext)d mod n = 383 269 mod 493 = 42
Public:
==0 _O/
/\/ ------------- 493,5 --------------> \
|\ /\_
/ | \ `
oo oo `
Cathy Heathcliff
==0_/ ,
/\_ <-------------- 383 --------------- /
|\ `\_\
/ | \
oo oo /O\
Cathy Heathcliff
Basic RSA algorithm for confidentiality:
- Ciphertext = (plaintext)e mod n
- Plaintext = (ciphertext)d mod n
- Private Key = {d, n}
- Public Key = {e, n}
Basic RSA algorithm for authentication:
- Ciphertext = (plaintext)d mod n
- Plaintext = (ciphertext)e mod n
- Private key = {d, n}
- Public key = {e, n}
RSA is the best possible type of public key cryptography, yet due to the high computation involved it is often not used to encrypt/decrypt simple messages. Instead, it’s used for signatures and protocol negotiations to allow two sides to receive private keys to use for their communication. The RSA algorithm is but one of many systems where a set of mathematical theorems, often from number theory, can be synthesised to construct an encryption scheme.
ElGamal
ElGamal is an algorithm used for transmitting digital signatures and key exchanges. The method is based on calculating logarithms. The algorithm is based on the characteristics of logarithmic numbers and calculations https://en.wikipedia.org/wiki/ElGamal_encryption. ElGamal is used in I2P garlic routing.
Digital Signature Algorithm (DSA)
The Digital Signature Algorithm (DSA) is based on the ElGamal algorithm and was developed by the United States government for digital signatures. DSA can be used only for signing data and it cannot be used for encryption. The DSA signing process is performed through a series of calculations based on a selected prime number. Although intended to have a maximum key size of 1,024 bits, longer key sizes are now supported https://en.wikipedia.org/wiki/Digital_Signature_Algorithm.
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography provides similar functionality to RSA and is implemented in smaller devices like cell phones, in TLS, PGP and SSH, and in Bitcoin and other cryptocurrencies. It requires less computing power than RSA. ECC encryption systems are based on the idea of using points on a curve to define the public/private key pair.
- DSA or Diffie-Hellman need a finite, cyclic group with the following characteristics:
- Group elements must be representable with relatively little memory.
- The group size must be known and be a prime number (or a multiple of a known prime number) of appropriate size (at least 160 bits for the traditional security level of "80-bit security").
- The group law must be easy to compute.
- It shall be hard (computationally infeasible, up to at least the targeted security level) to solve discrete logarithm in the group https://en.wikipedia.org/wiki/Discrete_logarithm.
- DH, ElGamal, DSA are primarily defined in the group of non-zero integers modulo a big prime
p, with modular multiplication as group law. The characteristics we look for are reached as long aspis large enough, at least 1024 bits (minimal size for discrete logarithm to be hard in such a group). - Elliptic curve are another kind of group useful for group-based cryptographic algorithms.
- An elliptic curve is defined with:
- A finite field https://en.wikipedia.org/wiki/Finite_field, usually consisting in integers modulo some prime
p(there are also other fields that can be used). - A curve equation, usually y2 = x3 + ax +b, where
aandbare constant values from the finite field.
- A finite field https://en.wikipedia.org/wiki/Finite_field, usually consisting in integers modulo some prime
- The curve is the set of pairs of values (x,y) which match the equation, along with a conventional extra element called the point at infinity. Since elliptic curves initially come from graphical representations (when the field consists in the real numbers
ℝ), the curve elements are called "points" and the two valuesxandyare their "coordinates". - Then we define a group law, called point addition and denoted with a
+sign. The definition looks quite artifical, with all the business about tracing a line and computing the intersection of that line with the curve; but the bottom-line is that it has the characteristics required for a group law, and it is easily computable (there are several methods; as a rough approximation, it costs about 10 multiplications in the base field).
Elliptic curves are said to be the next generation of cryptographic algorithms in order to replace RSA. The involved mathematics is a bit harder than with RSA, and there have been patents, so implementers are a bit wary. Yet elliptic curves appear to become more common.
Application examples
As of kernel version 2.5.45, the linux kernel includes the Crypto API, a cryptography framework for various parts of the kernel that deal with cryptography and includes essentially all popular block ciphers and hash functions https://www.kernel.org/doc/htmldocs/crypto-API/index.html.
Cryptographic hash functions
The key in public-key encryption is based on a hash value. This is a value that is computed from a base input number using a hashing algorithm. Essentially, the hash value is a summary of the original value. The important thing about a hash value is that it is nearly impossible to derive the original input number without knowing the data used to create the hash value.
Digital signatures
A digital signature is a way to ensure that an electronic document (email, spreadsheet, text file) is authentic. The Digital Signature Standard (DSS) is based on the Digital Signature Algorithm (DSA). DSS is the format for digital signatures that has been endorsed by the US government. If anything at all is changed in the document after the digital signature is attached to it, it changes the value that the digital signature compares to, rendering the signature invalid.
Digital certificates
A digital certificate is basically a unique piece of code or a large number that says that a Web server is trusted by an independent source known as a certificate authority. The certificate authority acts as a middleman that both computers trust. It confirms that each computer is in fact who it says it is, and then provides the public keys of each computer to the other.
TLS and its predecessor SSL use certificate authorities. Once your browser requests a secure page and adds the "s" onto "http", the browser sends out the public key and the certificate, checking three things:
- that the certificate comes from a trusted party
- that the certificate is currently valid
- that the certificate has a relationship with the site from which it's coming.
The browser then uses the public key to encrypt a randomly selected symmetric key. Public-key encryption takes a lot of computing, so most systems use a combination of public-key and symmetric key encryption. When two computers initiate a secure session, one computer creates a symmetric key and sends it to the other computer using public-key encryption. The two computers can then communicate using symmetric-key encryption. Once the session is finished, each computer discards the symmetric key used for that session. Any additional sessions require that a new symmetric key be created, and the process is repeated.
The Monkeysphere Project
Everyone who has used a web browser has been interrupted by the "Are you sure you want to connect?" warning message, which occurs when the browser finds the site's certificate unacceptable. But web browser vendors (e.g. Microsoft or Mozilla) should not be responsible for determining whom (or what) the user trusts to certify the authenticity of a website, or the identity of another user online. The user herself should have the final say, and designation of trust should be done on the basis of human interaction. The Monkeysphere project aims to make that possibility a reality http://web.monkeysphere.info/.
Cryptanalysis
Is cryptography still safe?
Translation of Is cryptografie nog wel veilig? by Jaap-Henk Hoepman http://blog.xot.nl/2013/09/09/is-cryptografie-nog-wel-veilig/
In response to the revelation that the NSA is trying to learn the contents of encrypted messages in many ways [3], Bruce Schneier gives some tips to stay safe [4](see the discussion on his blog [5]). However, his advice to use symmetric cryptography surprised me.
The main conclusions are the following. Both Schneier and Snowden say the NSA can not break strong cryptography immediately. The NSA can, however, access any possible device and thus get its hands on the data before it is encrypted. Implementations of cryptography in running systems may indeed be weak or made intentionally weak. For example, by building backdoors in telecom equipment [6]. The NSA also puts a lot of effort into that. This is also indirect evidence for the proposition that they can not directly crack cryptography itself.
There are many opportunities for placing backdoors. Especially if the encryption takes place in hardware (which is hard to check because it is a "black box"). For example, by making the cryptographic keys “less random” (less arbitrary) so they are easier to guess by the NSA. Or by leaking information about keys in the information stream the hardware generates. Another possibility is to design a system that is seemingly truly secure, but only for a small collection of keys.
In short, especially the implementation of cryptography gives problems.
That’s why it surprised me that Schneier gives the following advice: Prefer symmetric cryptography over public-key cryptography. Prefer conventional discrete-log-based systems over elliptic-curve systems; the latter have constants that the NSA influences when they can.
Symmetric cryptography over public key cryptography? That is exactly the opposite of what you would expect.
With symmetric cryptography sender and receiver use the same key. This means that it is difficult to ensure that you share a key with anyone who wants to send you a message, while no one else knows that key. In symmetric cryptosystems (DES and AES) message and key are mixed in an inextricable way. The way in which this is done is unfathomable, and there is no mathematical proof that the method is really safe.
In public key cryptography the receiver generates a pair of keys: a private key which is kept secret, and a corresponding public key that everyone can know. The public key is used to encrypt messages. The private key is required to decrypt messages. This (partly) solves the key distribution problem of symmetric cryptography. Public key cryptography is based on the (by mathematicians widely accepted) assumption that certain mathematical problems are difficult to solve. So hard to solve that a super fast computer can not solve it within, say, a 100 years. One such hard to solve problem is the decomposition of a number into prime factors. This RSA public key cryptosystem is based on that.
A survey yielded the following arguments for the surprising advice to prefer symmetric over public key cryptography:
- Schneier deems it more likely that the mathematical top talents of the NSA do (or have done) mathematical discoveries making public cryptosystems and the underlying difficult mathematical problems not so difficult to solve, then that they found something with which to break a symmetric cryptosystem.
- Public key cryptography does not really solve the key distribution problem. You still have to receive and know beforehand the public key of the person who is to receive the message. To solve this problem Certification Authorities (CA) were invented. These provide certificates stating what the public key of a particular person is. The most used and important CAs are American. So it is a breeze for the NSA to ensure that the certificates are incorrect and you use the wrong key. A key of the NSA. But the NSA does run a risk: other parties can see that the certificate is incorrect too. For example, this is how the DigiNotar hack was discovered.
- Public key cryptosystems have parameters that can be freely chosen, affecting the security of the system greatly. For some systems the effect of a particular choice is not clear. If a seemingly safe choice introduces weaknesses that (only) the NSA is aware of, this gives the NSA a way to crack it. Often the NSA directly or indirectly influences standards in which such particular choices are recorded. In the case of Elliptic Curve Cryptography (ECC) the most commonly used curves are recorded in American standards. Symmetric cryptosystems do not have such parameters, except for a limited choice in key length and block size.
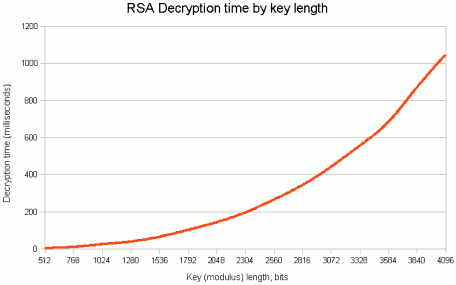
I do understand the distrust of ECC. However, the so-called discrete log systems and the on prime factorization based RSA system have a problem. More and faster algorithms are found that can solve the underlying mathematical problems. For a truly secure RSA the key should already be 2048 bits long. This is already quite unworkable large [7], and the question is when the key length must be further increased.
In other words, the shocking answer to the question whether cryptography is still safe is: yes, probably, but we do not know for sure, and our uncertainty is increased slightly after the revelations of the past few days. Unfortunately, there is no cryptosystem that we can prove to be really absolutely safe.
Notes
I keep saying this! There ***is*** a cryptosystem possible that can be proven to be really absolutely safe. It’s called one-time pads http://users.telenet.be/d.rijmenants/en/onetimepad.htm. It is not very practical, because OTPs require a key at least the length of the message to be encrypted and it can never be reused. Not very practical EXCEPT when you need provable security in an environment where you have access to an absolutely secure communications channel at one point, and need to send a message securely some time later.
Anyway, why did Bruce Schneier recommend symmetric over asymmetric? I think it is because the complete design of any cryptosystem shall be as transparent as possible, and that includes the generation of "seemingly random" parameters. His preference for symmetric cryptography over asymmetric cryptography seems based on asymmetric cryptography using parametrized mathematical objects and these parameters can be used to make the system weak. And probably have been. And he may be wearing multiple hats. Who knows?
I particularly enjoy what nightcracker wrote: Symmetric crypto is in a sense a lot more arcane, because there is a lot less math involved. It’s more like stirring a witch cauldron using explosive bullets fired by AK-47’s in the hope that it’s contents are so thoroughly mixed that only if you knew one part of the contents (the key) you can figure out the other (the message). As Bruce Schneier states he has more confidence in symmetric crypto, because we honestly have no idea how to crack these arcane mixing techniques.
Methinks Serpent (with some adaptations) an excellent base for that? Or twofish (Schneier)? Threefish (Schneier on the team)?
Is the clock ticking for encryption?
In "The clock is ticking for encryption" http://www.computerworld.com/article/2550008/security0/the-clock-is-ticking-for-encryption.html, Lamont Wood thinks the tidy world of cryptography may be upended by the arrival of quantum computers:
Today’s encryption algorithms can be broken. Their security derives from the wildly impractical lengths of time it can take to do so.
Let’s say you’re using a 128-bit AES cipher. The number of possible keys with 128 bits is 2 raised to the power of 128, or 3.4×1038, or 340 undecillion. Assuming no information on the nature of the key is available (such as the fact that the owner likes to use his or her children’s birthdays), a code-breaking attempt would require testing each possible key until one was found that worked.
Assuming that enough computing power was amassed to test 1 trillion keys per second, testing all possible keys would take 10.79 quintillion years. This is about 785 million times the age of the visible universe (13.75 billion years). On the other hand, you might get lucky in the first 10 minutes.
But using quantum technology with the same throughput, exhausting the possibilities of a 128-bit AES key would take about six months. If a quantum system had to crack a 256-bit key, it would take about as much time as a conventional computer needs to crack a 128-bit key.
A quantum computer could crack a cipher that uses RSA or EC algorithms almost immediately.
Resources
More movies
- Sebastian (1968) https://www.youtube.com/watch?v=bIK3OYnD9MY
News & watchdogs
- Anti-online http://www.antionline.com/
Cryptography
- Handbook of applied cryptography (2001, but a good resource) http://cacr.uwaterloo.ca/hac/
- Learning About Cryptography: A Basic Introduction to Crypto http://www.ciphersbyritter.com/LEARNING.HTM
- Ritter's Crypto Glossary and Dictionary of Technical Cryptography http://www.ciphersbyritter.com/GLOSSARY.HTM
Tools
- Exponents Calculator http://www.calculatorsoup.com/calculators/algebra/exponent.php
Symmetric
- A Stick Figure Guide to the Advanced Encryption Standard (AES) http://www.moserware.com/2009/09/stick-figure-guide-to-advanced.html
Asymmetric
- Hands-on Diffie–Hellman demonstration http://ds9a.nl/tmp/dh.html
- RSA: a simple and easy-to-read implementation (Python recipe) http://code.activestate.com/recipes/578838-rsa-a-simple-and-easy-to-read-implementation/
- Elliptic Curve Cryptography: a gentle introduction http://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
Digital signatures
- How Encryption and Digital Signatures Work http://www.tatanka.com/bionic_buffalo/original/archive/document/technote/tn0035.pdf
Monkeysphere
- What is the Monkeysphere? http://www.cracked.com/article_14990_what-monkeysphere.html
Cryptanalysis
- A Tutorial on Linear and Differential Cryptanalysis (from 2001, not overly mathematical) http://www.engr.mun.ca/~howard/PAPERS/ldc_tutorial.ps
- Cryptool portal https://www.cryptool.org (in english and/und auf deutsch)
Wiretapping
- Wiretapping http://www.crypto.com/papers/wiretapping/
Related
- Object encryption on linux
- Anonymising your traffic with linux
- Clean up all the things
- Wordsmithing
- Shell scripting
References
- ↑ How to destroy the internet http://gizmodo.com/5912383/how-to-destroy-the-internet
- ↑ Frequently Asked Questions (FAQ) About the Electronic Frontier Foundation's "DES Cracker" Machine https://w2.eff.org/Privacy/Crypto/Crypto_misc/DESCracker/HTML/19980716_eff_des_faq.html
- ↑ N.S.A. Able to Foil Basic Safeguards of Privacy on Web http://www.nytimes.com/2013/09/06/us/nsa-foils-much-internet-encryption.html
- ↑ NSA surveillance: A guide to staying secure http://www.theguardian.com/world/2013/sep/05/nsa-how-to-remain-secure-surveillance
- ↑ The NSA Is Breaking Most Encryption on the Internet http://www.schneier.com/blog/archives/2013/09/the_nsa_is_brea.html
- ↑ Secret Documents Reveal N.S.A. Campaign Against Encryption http://www.nytimes.com/interactive/2013/09/05/us/documents-reveal-nsa-campaign-against-encryption.html?ref=us&pagewanted=all
- ↑ RSA key lengths http://www.javamex.com/tutorials/cryptography/rsa_key_length.shtml