Difference between revisions of "Arcane mixing techniques"
From Gender and Tech Resources
m (→Debugging notes) |
m (→Projects) |
||
| (23 intermediate revisions by the same user not shown) | |||
| Line 123: | Line 123: | ||
The <code>NAND</code> and the <code>NOR</code> gate can be considered to be "universal" because you can make any of the basic operations out of its combinations: an inverter, an <code>OR</code> gate or an <code>AND</code> gate. Non-inverting gates do not have this versatility since they can not make an invert. | The <code>NAND</code> and the <code>NOR</code> gate can be considered to be "universal" because you can make any of the basic operations out of its combinations: an inverter, an <code>OR</code> gate or an <code>AND</code> gate. Non-inverting gates do not have this versatility since they can not make an invert. | ||
| + | |||
| + | === Labeling diagrams === | ||
| + | |||
| + | Integrated circuits have many individual circuit components in a single package. For example, the 7400 chip has 4 NAND gates. See resources for datasheets. | ||
| + | |||
| + | In the below circuit an <code>XOR</code> gate is created with NAND, NOR and NOT gates. Three chips are used: the 7400, 7402 and 7404. All inverters are on one chip. Both NAND's are on the same chip too. The chips are IC1, IC2 and IC3 in the diagram, the order in which they will be placed on the breadboard. Using gates located on one chip is also why the pins are numbered as they are (no need to look up datasheets while wiring). | ||
| + | |||
| + | These diagrams were made with SmartSim. | ||
| + | |||
| + | [[File:Labeling.png|800px|thumb|center]] | ||
| + | |||
| + | Simulated: | ||
| + | |||
| + | [[File:Xor00.png|700px|thumb|center]] | ||
| + | |||
| + | [[File:Xor01.png|700px|thumb|center]] | ||
| + | |||
| + | [[File:Xor11.png|700px|thumb|center]] | ||
== Wiring notes == | == Wiring notes == | ||
| Line 134: | Line 152: | ||
== Building gate circuits == | == Building gate circuits == | ||
| + | |||
| + | The resistors are sized to insure that the inverter circuit operates in digital mode. | ||
| + | |||
| + | For building the gate circuits, get: | ||
| + | * 2 pn2222 or 2 2n2222 transistors | ||
| + | * 1 ''1 KΩ'' resistor | ||
| + | * 2 ''33 kΩ'' resistor | ||
| + | * 2 LEDs | ||
| + | * 5V power | ||
=== Inverter circuit === | === Inverter circuit === | ||
| Line 199: | Line 226: | ||
== Boolean algebra == | == Boolean algebra == | ||
| − | == Minimisation with Morgan's laws == | + | === In plain english === |
| + | |||
| + | If "today is Monday'" is ''true'' then "Not(today is Monday)" is ''false''. This logical expression translates into English as "today is Not Monday" and this makes it easier to see that it is ''false'' if today is indeed Monday. Explanations like that rapidly become convoluted and difficult to follow and this is part of the power of Boolean logic. You can write down arguments in symbolic form. To simplify the handling of complex binary connectives, the mathematician George Boole developed Boolean Algebra, using ordinary algebraic notations AND, OR and NOT. Alternatives that you may encounter are ^ for AND, v for OR, and either over-score or prefix for NOT. | ||
| + | |||
| + | And ... The Boolean <code>AND</code> is the same as the English use of the term, but the Boolean <code>OR</code> is a little different: If you are asked "coffee OR tea?", in most western households you are not expected to say "yes" to both, while in the Boolean case <code>OR</code> includes both. The Boolean operator that corresponds to the English use of the term "OR" is the <code>XOR</code>. | ||
| + | |||
| + | The above tables next to the digital gates are called ''truth tables''. | ||
| + | === Burglary in progress === | ||
| + | Suppose you want to build a security system which only works at night and responds to a window or the front door being opened. If you have light sensors you can use these for giving off a signal indicating the truth of the statement: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Front door open !! Window open !! Burglary in progress | ||
| + | |- | ||
| + | | False || False || False | ||
| + | |- | ||
| + | | False || True || True | ||
| + | |- | ||
| + | | True || False || True | ||
| + | |- | ||
| + | | True || True || True | ||
| + | |} | ||
| + | |||
| + | We can make the propositions as complex as we want: | ||
| + | |||
| + | <pre>(Burglary in progress) = (NOT(It is daytime)) AND ((Window open) OR (Front door open)) | ||
| + | |||
| + | --------- | ||
| + | Front door open -----> | | | ||
| + | | OR |----- | ||
| + | Window open -----> | | | --------- | ||
| + | --------- +-----> | | | ||
| + | | AND |-----> Burglary in progress | ||
| + | --------- +-----> | | | ||
| + | | | | --------- | ||
| + | It is day time -----> | NOT |----- | ||
| + | | | | ||
| + | --------- | ||
| + | </pre> | ||
| + | |||
| + | === Precedence and maintaining order === | ||
| + | |||
| + | Boolean operations are carried out in a well defined order or "precedence": | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! Operator !! Symbol !! Precedence | ||
| + | |- | ||
| + | | NOT || ' || Highest | ||
| + | |- | ||
| + | | AND || . || Middle | ||
| + | |- | ||
| + | | OR || + || Lowest | ||
| + | |} | ||
| + | |||
| + | Expressions inside brackets are always evaluated first, overriding the default precedence order. The Boolean equation of the ''Burglary in progress'' block diagram in fully bracketed form: | ||
| + | <pre>B = ((T'). ((W) + (F)))</pre> | ||
| + | Using the precedence rules this can be simplified to: | ||
| + | |||
| + | <pre>B = T'. (W + F)</pre> | ||
| + | |||
| + | === Manipulating boolean expressions === | ||
| + | |||
| + | ==== Unary NOT ==== | ||
| + | |||
| + | And there are rules to manipulate Boolean expressions. The most simple are the rules for the unary operator NOT: | ||
| + | |||
| + | <pre>(A')' = A | ||
| + | A' . A = 0 | ||
| + | A' + A = 1</pre> | ||
| + | |||
| + | ==== General rules for AND and OR ==== | ||
| + | For more see Group theory Boolean Algebra http://mathworld.wolfram.com/BooleanAlgebra.html | ||
| + | |||
| + | Associative: | ||
| + | <pre>(A . B) .C = A . (B . C) | ||
| + | (A + B) + C = A + (B + C)</pre> | ||
| + | Commutative: | ||
| + | <pre>A . B = B . A | ||
| + | A + B = B + A</pre> | ||
| + | Distributive: | ||
| + | <pre>A . (B + C) = A . B + A . C | ||
| + | A + (B . C) = (A + B) . (A + C)</pre> | ||
| + | |||
| + | ==== Simplification rules ==== | ||
| + | |||
| + | The first group of simplification rules uses one variable: | ||
| + | |||
| + | <pre>A . A = A | ||
| + | A + A = A</pre> | ||
| + | |||
| + | The second group uses Boolean constants: | ||
| + | |||
| + | <pre>A . 0 = 0 | ||
| + | A . 1 = A | ||
| + | A + 0 = A | ||
| + | A + 1 = 1</pre> | ||
| + | |||
| + | ==== Example ==== | ||
| + | === Minimisation with Morgan's laws === | ||
== K-map groupings == | == K-map groupings == | ||
| Line 217: | Line 343: | ||
* Check minimisations and pinouts. | * Check minimisations and pinouts. | ||
* On rare occasions it is not me/you/us or what I/you/we did, and it is one of the components (a bent and curled pin, faulty chip, split wire (inside the insulation), faulty test equipment). If that turns out to be the case, don't kill component producer associated people. Or anybody else for that matter. | * On rare occasions it is not me/you/us or what I/you/we did, and it is one of the components (a bent and curled pin, faulty chip, split wire (inside the insulation), faulty test equipment). If that turns out to be the case, don't kill component producer associated people. Or anybody else for that matter. | ||
| − | + | == Projects == | |
| − | == | + | Notes on these projects are hosted on the [https://undisconnect.miraheze.org/wiki/Arcane_mixing_techniques UnDisConnect wiki]: |
| + | * A [https://undisconnect.miraheze.org/wiki/Greenhouse_sprinkler_system greenhouse sprinkler system]? Sure. Definitely not needs an arduino. That would be a tremendous overkill of resources. | ||
| + | * A [https://undisconnect.miraheze.org/wiki/4-bit_processor 4-bit processor]? Why not? If only to understand processor concepts and applied principles better. | ||
== Resources == | == Resources == | ||
| + | === Simulators === | ||
| + | |||
| + | * SmartSim http://smartsim.org.uk/downloads/manual/smartsim_user_manual.pdf (contains installation and getting started instructions. Because of glibc, I installed the stand-alone version) | ||
=== Breadboards === | === Breadboards === | ||
[[File:Cable-bus.png|300px|thumb|right]] | [[File:Cable-bus.png|300px|thumb|right]] | ||
| − | You can buy solderless breadboards in a shop or online. Mind that you pick scalable like the SD-12 so you can hook up breadboards together and they become reuseful for other projects such as prototyping our own | + | You can buy solderless breadboards in a shop or online. Mind that you pick scalable like the SD-12 so you can hook up breadboards together and they become reuseful for other projects such as prototyping our own embedded water management and short range radio (repeater) systems. |
Alternatively, start gathering and collecting IDC ribbon connectors (Floppy drive cables, old HD cables, SCSI cables) to build your own breadboards with. To do this, you will also need a solder iron, hot glue, wire (for example telephone wire will do), a small screw driver, and a clamp. This board will also be scalable. Fine grained scalable. :D | Alternatively, start gathering and collecting IDC ribbon connectors (Floppy drive cables, old HD cables, SCSI cables) to build your own breadboards with. To do this, you will also need a solder iron, hot glue, wire (for example telephone wire will do), a small screw driver, and a clamp. This board will also be scalable. Fine grained scalable. :D | ||
| Line 237: | Line 368: | ||
=== Light emitting diodes (LEDs) === | === Light emitting diodes (LEDs) === | ||
| − | === | + | === Transistors === |
| + | Transistors are three pin devices. The amount of current that can flow between the collector and emitter is a function of the current flowing through the base of the transistor. If no current is flowing through the base of the transistor, no current will flow through the collector and emitter. | ||
| + | * Transistors http://hyperphysics.phy-astr.gsu.edu/hbase/solids/trans.html#c1 | ||
| − | + | With the transistor operating in digital mode, it will be configured to carry the maximum (on) or minimum (off) current from the collector to the emitter that the circuit will allow. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | === Resistors === | |
| − | + | ||
| − | + | ||
| − | + | ||
=== Capacitors === | === Capacitors === | ||
| Line 260: | Line 386: | ||
* 2 V to 5 V = logic 1 | * 2 V to 5 V = logic 1 | ||
| − | The 7400 series logic chips have been manufactured since the 1960s and were used to design and build computers but they are no longer used for that. They still have many uses in teaching digital logic. They are easy to obtain and fairly inexpensive. They draw a lot of power and must be supplied with +5 volts. Individual gates may draw 3 to 4 mA. The low power Schottky versions of TTL chips draw only 20% of the power, but are more expensive. These chips have LS in the middle of their model number. | + | The 7400 series logic chips have been manufactured since the 1960s and were used to design and build computers but they are no longer used for that. They still have many uses in teaching digital logic. They are easy to obtain and fairly inexpensive. They draw a lot of power and must be supplied with +5 volts. Individual gates may draw 3 to 4 mA. The low power Schottky versions of TTL chips draw only 20% of the power, but are more expensive. These chips have LS in the middle of their model number. |
| − | + | * 7400 (Quad 2-Input NAND gate) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nand.html#c3 | |
| − | * 7400 (Quad 2-Input NAND gate) http:// | + | * 7402 (NOR, haven't found it yet) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nor.html#c3 |
| − | * 7402 (NOR, haven't found it yet) | + | * 7404 (Triple voltage regulator) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/buffer.html#c5 |
| − | * 7404 (Triple voltage regulator) http:// | + | |
* 7410 (Triple 3-Input NAND gate) http://pdf1.alldatasheet.com/datasheet-pdf/view/7823/NSC/7410.html | * 7410 (Triple 3-Input NAND gate) http://pdf1.alldatasheet.com/datasheet-pdf/view/7823/NSC/7410.html | ||
| + | * 7420 (Dual 4-Input NAND Gate) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nand3.html#c1 | ||
* 74151 (Data Selectors/Multiplexers) http://pdf1.alldatasheet.com/datasheet-pdf/view/7831/NSC/74151.html | * 74151 (Data Selectors/Multiplexers) http://pdf1.alldatasheet.com/datasheet-pdf/view/7831/NSC/74151.html | ||
* 74175 (Hex/Quad D Flip-Flops with Clear) http://pdf1.alldatasheet.com/datasheet-pdf/view/27396/TI/SN74175N.html | * 74175 (Hex/Quad D Flip-Flops with Clear) http://pdf1.alldatasheet.com/datasheet-pdf/view/27396/TI/SN74175N.html | ||
| − | * Timer (haven't found one yet) | + | * Timer (haven't found one yet) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/t555.html#c1 |
==== CMOS Logic ==== | ==== CMOS Logic ==== | ||
| Line 277: | Line 403: | ||
PMOS and NMOS ('''p'''- and '''n'''-channel '''m'''etal '''o'''xide '''s'''emiconductors) offer the advantage of higher component density than TTL chips. They too are sensitive to damage from electrical discharge. | PMOS and NMOS ('''p'''- and '''n'''-channel '''m'''etal '''o'''xide '''s'''emiconductors) offer the advantage of higher component density than TTL chips. They too are sensitive to damage from electrical discharge. | ||
| + | |||
| + | === Sensors === | ||
| + | |||
| + | Sensors can be video, sonar, radar, inductive, magnetic, capacitive, PVDF wire, pneumatic treadle. These use use significant electrical power, so each sensor must be connected to the power distribution network. New types of sensors can use magnetic technology. Clusters of such sensors transmit data to a receiver mounted on an electrical pole up to 300 meters away, which | ||
| + | relays the data to a processing station. The nodes can operate from a small internal lithium battery for at least 10 years and are vulnerable to heat and shock. | ||
== Related == | == Related == | ||
Latest revision as of 21:55, 29 September 2015
Contents
Digital techniques basics
For conceptual basics from the atomic level up see Semiconductors, Diodes and Transistors https://www.youtube.com/watch?v=wPHG0DCWcC0 AND An Introduction to Logic Gates https://www.youtube.com/watch?t=10&v=95kv5BF2Z9E.
Digital gates
AND
The AND gate behaves in the same way as the logical and operator: Output is true when both inputs are true and any otherwise false:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
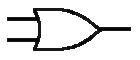
OR
The OR gate behaves like a logical inclusive or: Output is true if either or both of the inputs are true and false if both inputs are false:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
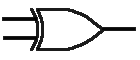
XOR
The XOR (exclusive-OR) gate acts as a logical either/or: the output is true if the inputs are different, and false if the inputs are the same:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
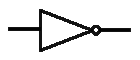
NOT
A logical inverter, alias NOT gate, has only one input and reverses logic state:
| Input 1 | Output |
|---|---|
| 0 | 1 |
| 1 | 0 |
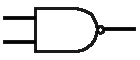
NAND
A NAND gate works like an AND gate followed by a NOT gate:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR
The NOR gate is a combination OR gate followed by an inverter:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XNOR
XNOR (exclusive-NOR) gate is a combination of an XOR gate followed by an inverter:
| Input 1 | Input 2 | Output |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Universal gates
The NAND and the NOR gate can be considered to be "universal" because you can make any of the basic operations out of its combinations: an inverter, an OR gate or an AND gate. Non-inverting gates do not have this versatility since they can not make an invert.
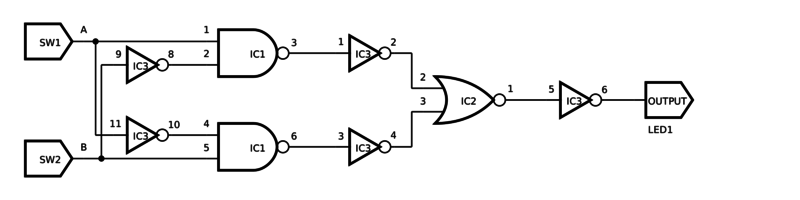
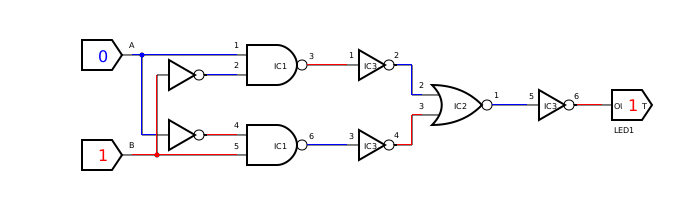
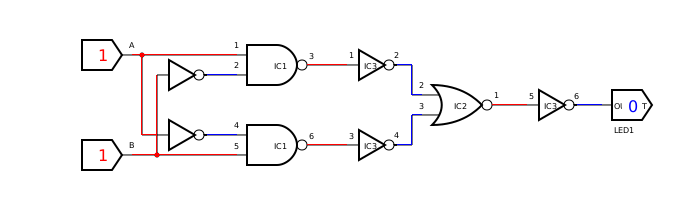
Labeling diagrams
Integrated circuits have many individual circuit components in a single package. For example, the 7400 chip has 4 NAND gates. See resources for datasheets.
In the below circuit an XOR gate is created with NAND, NOR and NOT gates. Three chips are used: the 7400, 7402 and 7404. All inverters are on one chip. Both NAND's are on the same chip too. The chips are IC1, IC2 and IC3 in the diagram, the order in which they will be placed on the breadboard. Using gates located on one chip is also why the pins are numbered as they are (no need to look up datasheets while wiring).
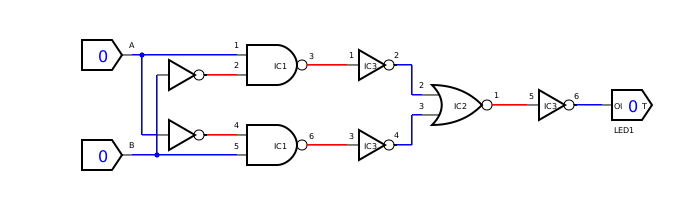
These diagrams were made with SmartSim.
Simulated:
Wiring notes
- Create (or have at hand) a circuit diagram before starting any wiring. Sketchy is okay.
- Use the longer outer rows for +5V on one side and ground on the other side.
- First wire power to the circuit using a common colour (red) for +5V and another (black) for ground.
- Power off while wiring circuits on the board.
- Maintain a clean household. In general designs tend to get complex and can become difficult to debug. The gate circuits are not but serpent definitely qualifies and good practice can not start soon enough (see Morgan's laws).
- Strip insulation off wires no more than necessary to prevent wires from accidentally touching each other.
- Do not push wires too far into holes to prevent causing open circuits or short circuits.
Building gate circuits
The resistors are sized to insure that the inverter circuit operates in digital mode.
For building the gate circuits, get:
- 2 pn2222 or 2 2n2222 transistors
- 1 1 KΩ resistor
- 2 33 kΩ resistor
- 2 LEDs
- 5V power
Inverter circuit
+ 5V ---------------------------+---------------------------->>
|
--------
| 1 KΩ |
--------
|--------------- LED
|
/
--------- |/
SW 1 ----------| 33 KΩ |-----| pn2222
--------- |\
\
|
GND ---------------------------+---------------------------->>
NAND circuit
If another transistor is added in series with the transistor in the inverter circuit, a NAND gate is created.
+ 5V ---------------------------+---------------------------->>
|
--------
| 1 KΩ |
--------
|--------------- LED
|
/
--------- |/
SW 1 ----------| 33 KΩ |-----| pn2222
--------- |\
\
|
/
--------- |/
SW 2 ----------| 33 KΩ |-----| pn2222
--------- |\
\
|
GND ---------------------------+---------------------------->>
NOR circuit
If another transistor is added in parallel with the transistor in the inverter circuit a NOR gate is the result. IOW, a NOR looks like two NOTs sharing a single pull-up transistor of 1 KΩ.
+ 5V ---------------------------+---------------------------->>
|
--------
| 1 KΩ |
--------
| +------------ LED
___|__|_
/ \
--------- |/ pn2222 \| ---------
SW 1 -----| 33 KΩ |-----| |-----| 33 KΩ |----- SW 2
--------- |\ pn2222 /| ---------
\_________/
|
GND ---------------------------+---------------------------->>
Boolean algebra
In plain english
If "today is Monday'" is true then "Not(today is Monday)" is false. This logical expression translates into English as "today is Not Monday" and this makes it easier to see that it is false if today is indeed Monday. Explanations like that rapidly become convoluted and difficult to follow and this is part of the power of Boolean logic. You can write down arguments in symbolic form. To simplify the handling of complex binary connectives, the mathematician George Boole developed Boolean Algebra, using ordinary algebraic notations AND, OR and NOT. Alternatives that you may encounter are ^ for AND, v for OR, and either over-score or prefix for NOT.
And ... The Boolean AND is the same as the English use of the term, but the Boolean OR is a little different: If you are asked "coffee OR tea?", in most western households you are not expected to say "yes" to both, while in the Boolean case OR includes both. The Boolean operator that corresponds to the English use of the term "OR" is the XOR.
The above tables next to the digital gates are called truth tables.
Burglary in progress
Suppose you want to build a security system which only works at night and responds to a window or the front door being opened. If you have light sensors you can use these for giving off a signal indicating the truth of the statement:
| Front door open | Window open | Burglary in progress |
|---|---|---|
| False | False | False |
| False | True | True |
| True | False | True |
| True | True | True |
We can make the propositions as complex as we want:
(Burglary in progress) = (NOT(It is daytime)) AND ((Window open) OR (Front door open))
---------
Front door open -----> | |
| OR |-----
Window open -----> | | | ---------
--------- +-----> | |
| AND |-----> Burglary in progress
--------- +-----> | |
| | | ---------
It is day time -----> | NOT |-----
| |
---------
Precedence and maintaining order
Boolean operations are carried out in a well defined order or "precedence":
| Operator | Symbol | Precedence |
|---|---|---|
| NOT | ' | Highest |
| AND | . | Middle |
| OR | + | Lowest |
Expressions inside brackets are always evaluated first, overriding the default precedence order. The Boolean equation of the Burglary in progress block diagram in fully bracketed form:
B = ((T'). ((W) + (F)))
Using the precedence rules this can be simplified to:
B = T'. (W + F)
Manipulating boolean expressions
Unary NOT
And there are rules to manipulate Boolean expressions. The most simple are the rules for the unary operator NOT:
(A')' = A A' . A = 0 A' + A = 1
General rules for AND and OR
For more see Group theory Boolean Algebra http://mathworld.wolfram.com/BooleanAlgebra.html
Associative:
(A . B) .C = A . (B . C) (A + B) + C = A + (B + C)
Commutative:
A . B = B . A A + B = B + A
Distributive:
A . (B + C) = A . B + A . C A + (B . C) = (A + B) . (A + C)
Simplification rules
The first group of simplification rules uses one variable:
A . A = A A + A = A
The second group uses Boolean constants:
A . 0 = 0 A . 1 = A A + 0 = A A + 1 = 1
Example
Minimisation with Morgan's laws
K-map groupings
Don't care conditions
Debugging notes
- If the errors show patterns of consistency, it's somewhere in the logic.
- If inconsistent, it's probably a loose connection.
- Test each component separately.
- Don't kill friends.
- Check power and GND for all appropriate pins.
- It can be frustrating. Don't kill family members.
- Check pin connections if done as specified in (sketchy) circuit diagram and that they aren't tied together.
- It can be very frustrating. Don't kill any acquaintances either.
- Check minimisations and pinouts.
- On rare occasions it is not me/you/us or what I/you/we did, and it is one of the components (a bent and curled pin, faulty chip, split wire (inside the insulation), faulty test equipment). If that turns out to be the case, don't kill component producer associated people. Or anybody else for that matter.
Projects
Notes on these projects are hosted on the UnDisConnect wiki:
- A greenhouse sprinkler system? Sure. Definitely not needs an arduino. That would be a tremendous overkill of resources.
- A 4-bit processor? Why not? If only to understand processor concepts and applied principles better.
Resources
Simulators
- SmartSim http://smartsim.org.uk/downloads/manual/smartsim_user_manual.pdf (contains installation and getting started instructions. Because of glibc, I installed the stand-alone version)
Breadboards
You can buy solderless breadboards in a shop or online. Mind that you pick scalable like the SD-12 so you can hook up breadboards together and they become reuseful for other projects such as prototyping our own embedded water management and short range radio (repeater) systems.
Alternatively, start gathering and collecting IDC ribbon connectors (Floppy drive cables, old HD cables, SCSI cables) to build your own breadboards with. To do this, you will also need a solder iron, hot glue, wire (for example telephone wire will do), a small screw driver, and a clamp. This board will also be scalable. Fine grained scalable. :D
I'll do both. Buy a few, and make a few.
Power supply
Switches for input
Light emitting diodes (LEDs)
Transistors
Transistors are three pin devices. The amount of current that can flow between the collector and emitter is a function of the current flowing through the base of the transistor. If no current is flowing through the base of the transistor, no current will flow through the collector and emitter.
With the transistor operating in digital mode, it will be configured to carry the maximum (on) or minimum (off) current from the collector to the emitter that the circuit will allow.
Resistors
Capacitors
Chips
TTL Logic
TTL (transistor-transistor-logic) chips were developed with use of transistor switches for logical operations and defines the binary values as:
- 0 V to 0.8 V = logic 0
- 2 V to 5 V = logic 1
The 7400 series logic chips have been manufactured since the 1960s and were used to design and build computers but they are no longer used for that. They still have many uses in teaching digital logic. They are easy to obtain and fairly inexpensive. They draw a lot of power and must be supplied with +5 volts. Individual gates may draw 3 to 4 mA. The low power Schottky versions of TTL chips draw only 20% of the power, but are more expensive. These chips have LS in the middle of their model number.
- 7400 (Quad 2-Input NAND gate) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nand.html#c3
- 7402 (NOR, haven't found it yet) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nor.html#c3
- 7404 (Triple voltage regulator) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/buffer.html#c5
- 7410 (Triple 3-Input NAND gate) http://pdf1.alldatasheet.com/datasheet-pdf/view/7823/NSC/7410.html
- 7420 (Dual 4-Input NAND Gate) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/nand3.html#c1
- 74151 (Data Selectors/Multiplexers) http://pdf1.alldatasheet.com/datasheet-pdf/view/7831/NSC/74151.html
- 74175 (Hex/Quad D Flip-Flops with Clear) http://pdf1.alldatasheet.com/datasheet-pdf/view/27396/TI/SN74175N.html
- Timer (haven't found one yet) http://hyperphysics.phy-astr.gsu.edu/hbase/electronic/t555.html#c1
CMOS Logic
CMOS (complementary metal oxide semiconductor) chips are lower in power requirements (drawing about 1 mA) and operate with a wide range of supply voltages (typically 3 to 18 volts). The CMOS model number will have a C in the middle of it. A bigh drawback is extreme sensitivity to static electricity - they must be carefully protected from static discharges.
NMOS and PMOS Logic
PMOS and NMOS (p- and n-channel metal oxide semiconductors) offer the advantage of higher component density than TTL chips. They too are sensitive to damage from electrical discharge.
Sensors
Sensors can be video, sonar, radar, inductive, magnetic, capacitive, PVDF wire, pneumatic treadle. These use use significant electrical power, so each sensor must be connected to the power distribution network. New types of sensors can use magnetic technology. Clusters of such sensors transmit data to a receiver mounted on an electrical pole up to 300 meters away, which relays the data to a processing station. The nodes can operate from a small internal lithium battery for at least 10 years and are vulnerable to heat and shock.